为了量化评估，我们引入具体的参数进行计算。假设某投影机恒温箱总重量为 。我们设计两种不同的吊挂方案：

• 方案A (刚性吊挂): 使用金属托架直接固定，其等效刚度 较高。假设其固有频率

• 方案B (弹性吊挂): 使用带弹簧减振器的吊挂，其等效刚度 较低。假设其固有频率   。

列车运行引起的振动频谱很宽，但我们主要关心其能量集中的 30-200 Hz 范围。取该范围内的一个代表性频率，例如 。

方案A:

频率比:   。

假设阻尼比 （钢结构典型值）。

传递率 :

这表明，即使在共振区外，刚性吊挂仍有34%的振动被传递。

方案B:

频率比: 。

传递率 :

这表明，弹性吊挂只传递了20%的振动，隔离效果比刚性吊挂提高了约41%。

我们还可以计算加速度。假设轨道结构的振动加速度均方根值（RMS）为 (约0.1g)。那么，经过吊挂传递后，设备所受的加速度 。

• 方案A:

• 方案B:

这个加速度水平虽然看似不大，但对于需要长期稳定工作的精密光学设备而言，持续的振动累积效应不容忽视。它会导致光学元件的微小位移和形变，影响光束的准直性。

为了验证理论模型，我们可以参考已有的现场实测数据。一项针对北京某数据中心受地铁4号线振动影响的评估研究，在距离隧道中心线24米处的测点，测得列车通过时的垂向振动加速度峰值高达 3.0 cm/s² (即0.03g) [4]。另一项在实验室条件下，通过激振台对投影机进行的振动测试（GB/T 2423.10标准）中，通常会施加高达 1.5g 的加速度来模拟运输过程的严酷条件 [7]。虽然运行环境的振动水平低于运输测试，但长期暴露在这样的振动环境中，足以引发疲劳损伤和性能漂移。

3.4 仿真分析与影响评估

理论分析和公式计算为我们提供了基础，而有限元分析（FEA）则能更精细地模拟整个系统的动力学行为。我们可以利用ANSYS软件建立模型：

我们可以利用ANSYS软件建立模型：

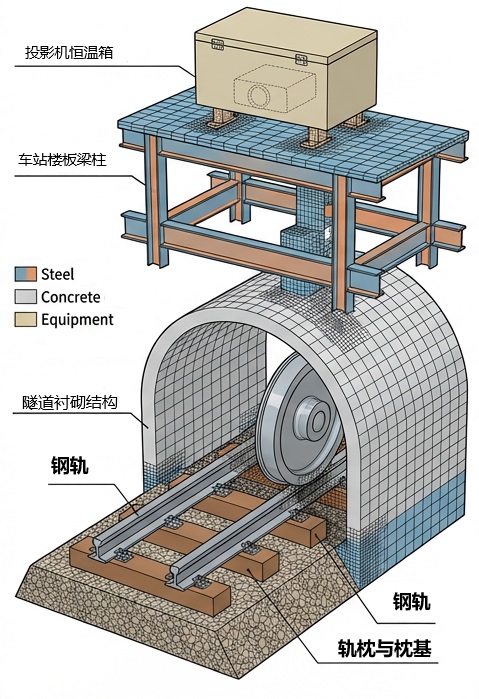
有限元分析模型

1.  建立轨道-隧道-建筑-设备模型：创建钢轨、轨枕、隧道衬砌、车站楼板梁柱以及投影机恒温箱的详细三维模型，并赋予相应的材料属性（密度、弹性模量、泊松比）。

2.  网格划分：对模型进行网格划分，在关注区域（如轮轨接触区、设备固定点）进行网格细化，以确保计算精度。

 3.  施加边界条件与载荷：在模型底部施加固定约束，模拟隧道基础。在车轮与钢轨的接触点施加实测或仿真的轮轨力时程曲线作为动态载荷。