列车在轨道上运行是轨道交通系统中最为持续和强烈的振动源。这种振动源于轮轨相互作用，并通过轨道结构、隧道衬砌、土体介质，最终传递到隧道壁及附属结构上，对沿线设备构成环境振动激励。本章节将首先阐述列车运行振动的产生机理与频域特性，然后基于结构动力学理论，建立从轨道到投影机安装点的振动传递模型，并利用公式进行量化评估，最后通过现场实测数据与数值仿真进行验证，从而系统分析其对投影机性能的潜在影响。

3.1 振动产生机理与频域特性

列车运行时引发的振动是一个复杂的多体动力学问题。其主要激励源包括：1) 轨道不平顺：这是最主要的激励源。钢轨的几何形位偏差（如高低、水平、轨向、扭曲等）在车轮经过时会产生动态冲击力。根据波长和幅值的不同，轨道不平顺可分为周期性不平顺（如焊缝、接头等）和随机性不平顺。高速铁路和城市轨道交通普遍铺设无缝线路，但焊接接头、道岔等仍然是轨道短波不平顺的主要来源。2) 车轮不圆顺：车轮在制造和使用过程中会产生偏心、椭圆、擦伤等几何缺陷，这些缺陷在转动时会产生周期性的离心激励力，其频率与车速和车轮半径相关。3) 轨道结构振动：轮轨冲击力作用于钢轨，引发钢轨、轨枕、道床乃至下部结构（隧道或路基）的垂向和横向振动。这些振动以波的形式在结构中传播，其能量主要集中在特定频段。4) 列车动力系统：牵引电机、齿轮箱、联轴器等旋转部件的不平衡力也会产生一定量的振动，但其主要频率通常较高，对低频环境振动贡献相对较小。

现场实测与大量研究表明，地铁列车运行引起的地面及隧道结构振动，其频域特性主要集中于 10 Hz - 200 Hz 范围内 [4]。其中， 20 Hz - 80 Hz 是能量最为集中的频段，也是对人体舒适度和精密设备影响最大的频率范围。例如，一项在深圳进行的现场测试显示，双线地铁运行时，隧道壁及附近地面的振动主频集中在 40 Hz - 70 Hz [5]。另一项针对南昌地铁3号线的分析也指出，列车引起的隧道振动峰值频率出现在 63 Hz 附近 [6]。这些振动能量通过隧道结构传递至站厅、出入口以及轨行区上方的建筑结构，导致这些建筑结构产生“整体振动”，进而通过吊挂支架或预埋件传递给投影机恒温箱。特别值得关注的是，振动在传递过程中可能会出现“频率漂移”和“放大效应”。当结构（如楼板、梁、吊架）的固有频率与激励频率（如列车振动的某些主频）接近或重合时，会发生共振，导致该位置的振动加速度被显著放大，可能达到输入激励的数倍，这对设备的危害极大。

3.2 振动传递路径与动力学模型

从振源（车轮/轨道）到投影机（受振体）的振动传递是一个典型的“振源-传播路径-接收者”系统。我们可以将其简化为一个多自由度（MDOF）弹簧-质量-阻尼系统。为了进行理论分析，我们建立一个简化的垂向振动模型，如图所示：

[列车车轮] ： k1,c1 ；        [钢轨] ： k2,c2 ；         [轨枕/道床] ： k3,c3 ：

[隧道结构] ： k4,c4 ；    [建筑结构] ： k5,c5 ；   [投影机恒温箱] ： m (设备质量)；

其中：

m 代表投影机及恒温箱的总质量。

k_i 和 c_i (i=1...5) 分别代表各传递路径的等效刚度和阻尼系数。

k5, c5 代表最后的吊挂或支撑结构的刚度和阻尼。

该系统的运动方程可以表示为：

其中：

[M], [C], [K] 是质量、阻尼和刚度矩阵，{x} 是位移向量，F(t)是列车轮轨力施加激振力向量。

对于这样一个复杂的系统，直接求解较为困难。通常，我们可以通过模态分析来理解其动态特性。系统的各阶固有频率 ω_n 和振型 φ 满足特征方程：

当激振频率 ω 接近系统的任一阶固有频率 ω_n 时，系统将发生共振，响应幅值急剧增大。阻尼比 ζ 的大小决定了共振峰的尖锐程度，ζ 越小，共振峰越尖锐，放大效应越强。

我们可以关注最后一个环节，即吊挂系统。这部分可以简化为一个单自由度系统（SDOF）：

其中 m 是设备总质量，k 是吊挂装置的刚度，c 是阻尼。 该系统的位移传递率 T_d（输出位移幅值与输入位移幅值之比）为：

其中：

.............是频率比，

............是系统的固有频率，

............是阻尼比。

这个公式揭示了振动隔离的关键：

当 r > sqrt(2) (即 ω > sqrt(2)*ω_n) 时，T_d < 1，系统具有隔振效果。频率比 r 越大，隔振效果越好。这意味着，为了有效隔离列车运行产生的高频振动，吊挂系统的固有频率 ω_n 应该设计得足够低。例如，如果列车激振的主要频率分量集中在 30 Hz 以上，那么我们可以将吊挂系统的固有频率设计在 10 Hz 左右，这样在 30 Hz 以上频段内就能获得良好的隔振效果。

3.3 公式计算与数据验证

为了量化评估，我们引入具体的参数进行计算。假设某投影机恒温箱总重量为 。我们设计两种不同的吊挂方案：

• 方案A (刚性吊挂): 使用金属托架直接固定，其等效刚度 较高。假设其固有频率

• 方案B (弹性吊挂): 使用带弹簧减振器的吊挂，其等效刚度 较低。假设其固有频率   。

列车运行引起的振动频谱很宽，但我们主要关心其能量集中的 30-200 Hz 范围。取该范围内的一个代表性频率，例如 。

方案A:

频率比:   。

假设阻尼比 （钢结构典型值）。

传递率 :

这表明，即使在共振区外，刚性吊挂仍有34%的振动被传递。

方案B:

频率比: 。

传递率 :

这表明，弹性吊挂只传递了20%的振动，隔离效果比刚性吊挂提高了约41%。

我们还可以计算加速度。假设轨道结构的振动加速度均方根值（RMS）为 (约0.1g)。那么，经过吊挂传递后，设备所受的加速度 。

• 方案A:

• 方案B:

这个加速度水平虽然看似不大，但对于需要长期稳定工作的精密光学设备而言，持续的振动累积效应不容忽视。它会导致光学元件的微小位移和形变，影响光束的准直性。

为了验证理论模型，我们可以参考已有的现场实测数据。一项针对北京某数据中心受地铁4号线振动影响的评估研究，在距离隧道中心线24米处的测点，测得列车通过时的垂向振动加速度峰值高达 3.0 cm/s² (即0.03g) [4]。另一项在实验室条件下，通过激振台对投影机进行的振动测试（GB/T 2423.10标准）中，通常会施加高达 1.5g 的加速度来模拟运输过程的严酷条件 [7]。虽然运行环境的振动水平低于运输测试，但长期暴露在这样的振动环境中，足以引发疲劳损伤和性能漂移。

3.4 仿真分析与影响评估

理论分析和公式计算为我们提供了基础，而有限元分析（FEA）则能更精细地模拟整个系统的动力学行为。我们可以利用ANSYS软件建立模型：

我们可以利用ANSYS软件建立模型：

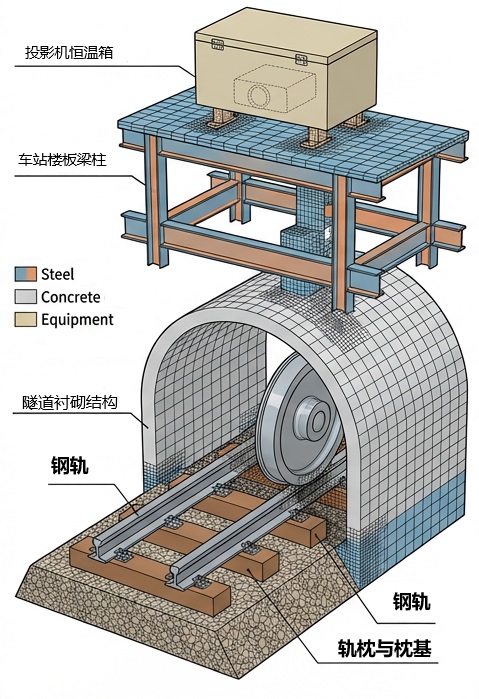
有限元分析模型

1.  建立轨道-隧道-建筑-设备模型：创建钢轨、轨枕、隧道衬砌、车站楼板梁柱以及投影机恒温箱的详细三维模型，并赋予相应的材料属性（密度、弹性模量、泊松比）。

2.  网格划分：对模型进行网格划分，在关注区域（如轮轨接触区、设备固定点）进行网格细化，以确保计算精度。

 3.  施加边界条件与载荷：在模型底部施加固定约束，模拟隧道基础。在车轮与钢轨的接触点施加实测或仿真的轮轨力时程曲线作为动态载荷。

4.  进行谐响应分析或瞬态动力学分析：

    -   谐响应分析：在感兴趣的频率范围内（如5-200Hz），计算系统各点的响应（位移、速度、加速度）随频率的变化，从而找到共振频率和放大因子。

    -   瞬态动力学分析：施加一个完整的列车通过载荷时程，模拟设备在整个事件中的振动响应历程，可以得到最大响应值和响应的时域分布。

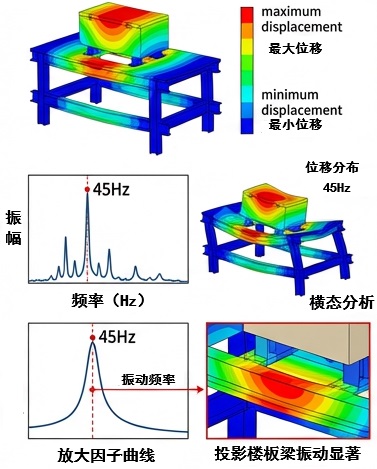
受力分析

通过仿真，我们可以清晰地看到振动能量是如何从轨道向上传递，在楼板中如何分布，以及在设备固定点处的响应大小。例如，仿真可能揭示，某个特定的楼板梁由于其第一阶弯曲模态频率（如45Hz）与列车激振的主要频率分量（40-50Hz）非常接近，导致了该梁的显著振动，进而使得安装在其下的投影机也产生了较大的晃动。

最终，这些振动对投影机性能的影响体现在：

-   光学校准漂移：光学平台、镜头筒体的微小变形或振动，会改变光轴方向和像面位置，导致画面聚焦不准、清晰度下降。

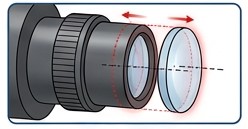
像素抖动与图像模糊：对于DLP或LCD芯片，如果其安装基座发生振动，会使得微镜或像素单元产生附加的物理运动，导致图像边缘模糊、细节丢失。

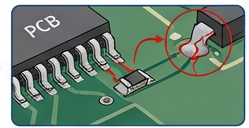
连接器与焊点疲劳：长期的振动循环应力会导致电路板上的连接器、芯片引脚以及焊点等机械薄弱环节发生疲劳断裂，造成设备间歇性故障或永久性损坏。

综上所述，列车运行产生的环境振动是影响轨行区投影机稳定性的首要因素。其振动能量通过复杂的结构路径传递，并在特定频率下可能被放大，对投影机的光学性能、机械结构和电气连接都构成严重威胁。因此，在系统设计和设备选型时，必须对这一振动源给予高度重视，并采取有效的隔离与控制措施。